Zohar Nussinov and colleagues have created a computer algorithm to tackle one of physics’ most enduring mysteries.
Zohar Nussinov, professor of physics, and graduate student Mutian Shen have contributed to a significant advance in the understanding of “spin glasses,” a class of mysterious materials that has intrigued and confounded physicists for decades. Their insights, reported in Nature Communications, could have applications outside of physics, including an improved understanding of complex systems like neural networks.
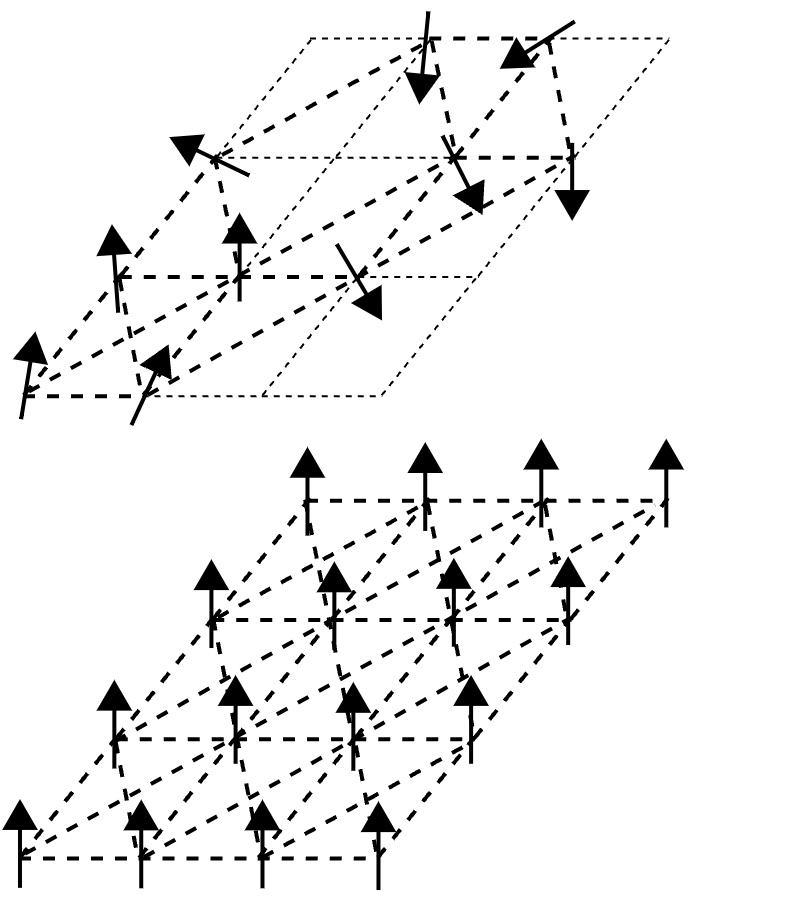
Magnetic ions such as iron have magnetic moments. These moments can be thought of as tiny magnetic compass needles. In most common magnets, like the ones stuck to a refrigerator, these compass needles tend to align in the same direction as their neighbors.
But spin glasses — created by randomly mixing iron or other magnetic ions with non-magnetic metals, like gold or copper — are too disordered for simple decisions. Pushed and pulled in different directions by their scattered neighbors, the needles don’t know which way to point. With so many random interactions happening at once, spin glasses are much more complicated and beguiling than simple fridge magnets.
For decades, the properties of spin glasses have served as ideal fodder for researchers from numerous disciplines who want to understand complex systems. Trying to find the arrangement where the maximum number of magnetic ions are optimally aligned with their neighbors — known as a low-energy state — is a bit like planning moves on a chessboard, Nussinov said, only with more squares and pieces. “It’s easy to pose a problem, but it's hard to find a solution,” he said. “We’ve found a way to do that very quickly.”
Spin glasses are already a Nobel-worthy topic. In 2021, Italian theoretical physicist Giorgio Parisi shared the physics prize for creating a mathematical approach to spin glass that studied these systems in an effectively infinite number of spatial dimensions.
Nussinov, Shen, and colleagues have created a deep learning computer algorithm to describe a more realistic model with short-range interactions in a finite number of dimensions. The algorithm, called DIRAC (deep reinforcement learning for spin-glass ground state calculation) considers what would happen when magnetic atoms are tugged in different directions by several neighbors simultaneously. While a small number of neighbors may seem like a simpler scenario than Parisi’s infinite interactions, the nature of spin glasses becomes much more complicated in real, 3D spaces where Parisi’s analysis no longer directly applies, Nussinov said.
It would take an astronomical amount of time to calculate the ideal low-energy or “ground” state of all atoms in large spin glass systems. Shen explained that, just like playing chess, DIRAC is designed to look at the big-picture of the system as a whole, not just optimizing the arrangement of a few magnetic moments magnet by magnet. “It’s looking at the long-term reward, not the short term,” he said.
The algorithm also calls upon a crucially important concept in physics known as “gauge symmetry.” Thanks to this symmetry, the algorithm can quickly leapfrog between vastly different configurations in different spin glass systems. By applying gauge symmetry operations multiple times, DIRAC more successfully avoids getting stuck in a dead-end configuration that may not lead to the ultimate goal of finding the lowest possible energy state.
The same basic principles behind DIRAC could potentially be applied to other systems of high complexity, Nussinov said. For example, a better understanding of the microscopic magnetic needles in spin glasses could shed light on other entities influenced by multiple neighbors, like individual neurons in neural networks. And in much the same way that DIRAC can search for low-energy spin glass configurations, the cells in our bodies have to fold proteins in just the right way to minimize conflict. “There are a lot of situations in biology where the final energy state is crucially important,” he said.
Nobody knows exactly how nature accomplishes such computational feats, but it clearly happens. That, Nussinov says, is one of the lessons of spin glasses: Even the most complex problems can have natural, elegant solutions.



